ml_linalg 12.16.0

SIMD-based linear algebra and statistics for data science

SIMD-based linear algebra and statistics for data science with Dart

Table of contents

• What is linear algebra
• What is SIMD
• Vectors
  • A couple of words about the underlying architecture
    • Vector benchmarks
    • Vector operations
      • Vectors sum
      • Vectors subtraction
      • Element-wise vector by vector multiplication
      • Element-wise vector by vector division
      • Euclidean norm
      • Manhattan norm
      • Mean value
      • Sum of all vector elements
      • Product of all vector elements
      • Element-wise power
      • Element-wise exp
      • Dot product
      • Sum of a vector and a scalar
      • Subtraction of a scalar from a vector
      • Multiplication of a vector by a scalar
      • Division of a vector by a scalar
      • Euclidean distance between two vectors
      • Manhattan distance between two vectors
      • Cosine distance between two vectors
      • Vector normalization (using Euclidean norm)
      • Vector normalization (using Manhattan norm)
      • Vector rescaling (min-max normalization)
      • Vector serialization
      • Vector mapping
• Matrices
  • Matrix operations
    • Creation of diagonal matrix
    • Creation of scalar matrix
    • Creation of identity matrix
    • Creation of column matrix
    • Creation of row matrix
    • Sum of a matrix and another matrix
    • Sum of a matrix and a scalar
    • Multiplication of a matrix and a vector
    • Multiplication of a matrix and another matrix
    • Multiplication of a matrix and a scalar
    • Hadamard product (element-wise matrices multiplication)
    • Element-wise matrices subtraction
    • Matrix transposition
    • Matrix row-wise reduce
    • Matrix column-wise reduce
    • Matrix row-wise mapping
    • Matrix column-wise mapping
    • Matrix element-wise mapping
    • Getting max value of the matrix
    • Getting min value of the matrix
    • Matrix element-wise power
    • Matrix element-wise exp
    • Sum of all matrix elements
    • Product of all matrix elements
    • Matrix indexing and sampling
    • Add new columns to a matrix
    • Matrix serialization/deserialization
• Contacts

Linear algebra

In a few words, linear algebra is a branch of mathematics that is working with vectors and matrices.

Let's give a simple definition of Vector and Matrix. Vector is an ordered set of numbers representing a point in the space where the vector is directed from the origin. Matrix is a collection of vectors that is used to map vectors from one space to another.

Vectors and matrices are extremely powerful tools which can be used in real-life applications, such as machine learning algorithms. There are many implementations of these great mathematical entities in a plenty of programming languages, and as Dart offers developers good instrumentarium, e.g. highly optimized virtual machine and rich out-of-the-box library, Dart-based implementation of vectors and matrices has to be quite performant.

Among myriad of standard Dart tools there are SIMD data types. Namely support of SIMD computational architecture served as a source of inspiration for creating this library.

What is SIMD?

SIMD stands for Single instruction, multiple data - it's a computer architecture that allows to perform uniform mathematical operations in parallel on a list-like data structure. For instance, one has two arrays:

• 
• 

and one needs to add these arrays element-wise. Using the regular architecture this operation could be done in the following manner:

We need to do 4 operations one by one in a row. Using SIMD architecture we may perform one mathematical operation on several operands in parallel, thus element-wise sum of two arrays will be done for just one step:

Vectors

A couple of words about the underlying architecture

The library contains two high performant vector classes based on Float32x4 and Float64x2 data types - Float32x4Vector and Float64x2Vector (the second one is generated from the source code of the first vector's implementation)

Most of element-wise operations in the first one are performed in four "threads" and in the second one - in two "threads".

Implementation of both classes is hidden from the library's users. You can create a Float32x4Vector or a Float64x2Vector instance via Vector factory (see examples below).

The vectors are immutable: once created, the vector cannot be changed. All the vector operations lead to creation of a new vector instance (of course, if the operation is supposed to return a Vector).

Both classes implement Iterable<double> interface, so it's possible to use them as regular iterable collections.

It's possible to use vector instances as keys for HashMap and similar data structures and to look up a value by the vector-key, since the hash code is the same for equal vectors:

import 'package:ml_linalg/vector.dart';

final map = HashMap<Vector, bool>();

map[Vector.fromList([1, 2, 3, 4, 5])] = true;

print(map[Vector.fromList([1, 2, 3, 4, 5])]); // true
print(Vector.fromList([1, 2, 3, 4, 5]).hashCode == Vector.fromList([1, 2, 3, 4, 5]).hashCode); // true

Vector benchmarks

To see the performance benefits provided by the library's vector classes, one may visit benchmark directory: one may find there a baseline benchmark - element-wise summation of two regular List instances and a benchmark of a similar operation, but performed on two Float32x4Vector instances on the same amount of elements and compare the timings:

• Baseline benchmark (executed on Macbook Air mid 2017), 2 regular lists each with 10,000,000 elements:

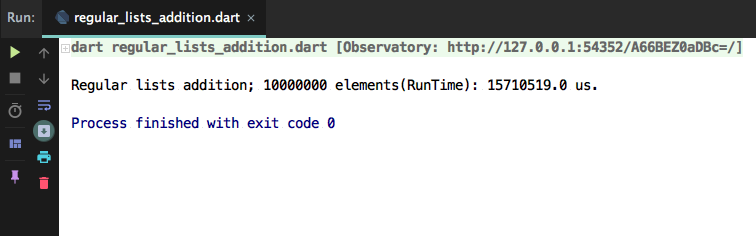
• Actual benchmark (executed on Macbook Air mid 2017), 2 vectors each with 10,000,000 elements:

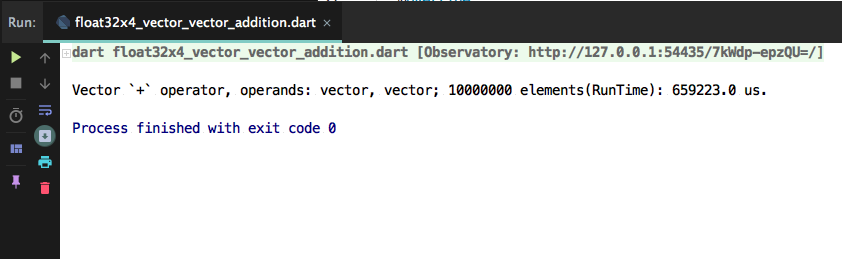
It took 15 seconds to create a new regular list by summing the elements of two lists, and 0.7 second to sum two vectors - the difference is significant.

Vector operations examples

Vectors sum

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1 + vector2;

  print(result.toList()); // [3.0, 5.0, 7.0, 9.0, 11.0]

Vectors subtraction

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([4.0, 5.0, 6.0, 7.0, 8.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 2.0, 3.0, 2.0]);
  final result = vector1 - vector2;

  print(result.toList()); // [2.0, 2.0, 4.0, 4.0, 6.0]

Element wise vector by vector multiplication

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1 * vector2;

  print(result.toList()); // [2.0, 6.0, 12.0, 20.0, 30.0]

Element wise vector by vector division

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([6.0, 12.0, 24.0, 48.0, 96.0]);
  final vector2 = Vector.fromList([3.0, 4.0, 6.0, 8.0, 12.0]);
  final result = vector1 / vector2;

  print(result.toList()); // [2.0, 3.0, 4.0, 6.0, 8.0]

Euclidean norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.norm();

  print(result); // sqrt(2^2 + 3^2 + 4^2 + 5^2 + 6^2) = sqrt(90) ~~ 9.48

Manhattan norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.norm(Norm.manhattan);

  print(result); // 2 + 3 + 4 + 5 + 6 = 20.0

Mean value

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.mean();

  print(result); // (2 + 3 + 4 + 5 + 6) / 5 = 4.0

Sum of all vector elements

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.sum();

  print(result); // 2 + 3 + 4 + 5 + 6 = 20.0

Product of all vector elements

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.prod();

  print(result); // 2 * 3 * 4 * 5 * 6 = 720

Element-wise power

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.pow(3);
  
  print(result); // [2 ^ 3 = 8.0, 3 ^ 3 = 27.0, 4 ^ 3 = 64.0, 5 ^3 = 125.0, 6 ^ 3 = 216.0]

Element-wise exp

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.exp();
  
  print(result); // [e ^ 2, e ^ 3, e ^ 4, e ^ 5, e ^ 6]

Dot product of two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.dot(vector2);

  print(result); // 1.0 * 2.0 + 2.0 * 3.0 + 3.0 * 4.0 + 4.0 * 5.0 + 5.0 * 6.0 = 70.0

Sum of a vector and a scalar

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final scalar = 5.0;
  final result = vector1 + scalar;

  print(result.toList()); // [6.0, 7.0, 8.0, 9.0, 10.0]

Subtraction of a scalar from a vector

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final scalar = 5.0;
  final result = vector - scalar;

  print(result.toList()); // [-4.0, -3.0, -2.0, -1.0, 0.0]

Multiplication of a vector by a scalar

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final scalar = 5.0;
  final result = vector * scalar;

  print(result.toList()); // [5.0, 10.0, 15.0, 20.0, 25.0]

Division of a vector by a scalar

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([25.0, 50.0, 75.0, 100.0, 125.0]);
  final scalar = 5.0;
  final result = vector.scalarDiv(scalar);

  print(result.toList()); // [5.0, 10.0, 15.0, 20.0, 25.0]

Euclidean distance between two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.distanceTo(vector2, distance: Distance.euclidean);

  print(result); // ~~2.23

Manhattan distance between two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.distanceTo(vector2, distance: Distance.manhattan);

  print(result); // 5.0

Cosine distance between two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.distanceTo(vector2, distance: Distance.cosine);

  print(result); // 0.00506

Vector normalization using Euclidean norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final result = vector.normalize(Norm.euclidean);

  print(result); // [0.134, 0.269, 0.404, 0.539, 0.674]

Vector normalization using Manhattan norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0]);
  final result = vector.normalize(Norm.manhattan);

  print(result); // [0.066, -0.133, 0.200, -0.266, 0.333]

Vector rescaling (min-max normalization)

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0, 0.0]);
  final result = vector.rescale();

  print(result); // [0.555, 0.222, 0.777, 0.0, 1.0, 0.444]

Vector serialization

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0, 0.0]);
  final serialized = vector.toJson();
  print(serialized); // it yields a serializable representation of the vector

  final restoredVector = Vector.fromJson(serialized);
  print(restoredVector); // [1.0, -2.0, 3.0, -4.0, 5.0, 0.0]

Vector mapping

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0, 0.0]);
  final mapped = vector.mapToVector((el) => el * 2);
  
  print(mapped); // [2.0, -4.0, 6.0, -8.0, 10.0, 0.0]
  print(mapped is Vector); // true
  print(identical(vector, mapped)); // false

Matrices

Along with SIMD vectors, the library presents SIMD-based Matrices. One can use the matrices via Matrix factory. The matrices are immutable as well as vectors and also they implement Iterable interface (to be precise, Iterable<Iterable<double>>), thus it's possible to use them as a regular iterable collection.

Matrices are serializable, and that means that one can easily convert a Matrix instance to a json-serializable map via toJson method, see the examples below.

Matrix operations examples

Creation of diagonal matrix

import 'package:ml_linalg/matrix.dart';

final matrix = Matrix.diagonal([1, 2, 3, 4, 5]);

print(matrix);

The output:

Matrix 5 x 5:
(1.0, 0.0, 0.0, 0.0, 0.0)
(0.0, 2.0, 0.0, 0.0, 0.0)
(0.0, 0.0, 3.0, 0.0, 0.0)
(0.0, 0.0, 0.0, 4.0, 0.0)
(0.0, 0.0, 0.0, 0.0, 5.0)

Creation of scalar matrix

import 'package:ml_linalg/matrix.dart';

final matrix = Matrix.scalar(3, 5);

print(matrix);

The output:

Matrix 5 x 5:
(3.0, 0.0, 0.0, 0.0, 0.0)
(0.0, 3.0, 0.0, 0.0, 0.0)
(0.0, 0.0, 3.0, 0.0, 0.0)
(0.0, 0.0, 0.0, 3.0, 0.0)
(0.0, 0.0, 0.0, 0.0, 3.0)

Creation of identity matrix

import 'package:ml_linalg/matrix.dart';

final matrix = Matrix.identity(5);

print(matrix);

The output:

Matrix 5 x 5:
(1.0, 0.0, 0.0, 0.0, 0.0)
(0.0, 1.0, 0.0, 0.0, 0.0)
(0.0, 0.0, 1.0, 0.0, 0.0)
(0.0, 0.0, 0.0, 1.0, 0.0)
(0.0, 0.0, 0.0, 0.0, 1.0)

Creation of column matrix

final matrix = Matrix.column([1, 2, 3, 4, 5]);

print(matrix);

The output:

Matrix 5 x 1:
(1.0)
(2.0)
(3.0)
(4.0)
(5.0)

Creation of row matrix

final matrix = Matrix.row([1, 2, 3, 4, 5]);

print(matrix);

The output:

Matrix 1 x 5:
(1.0, 2.0, 3.0, 4.0, 5.0)

Sum of a matrix and another matrix

import 'package:ml_linalg/linalg.dart';

final matrix1 = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
final matrix2 = Matrix.fromList([
  [10.0, 20.0, 30.0, 40.0],
  [-5.0, 16.0, 2.0, 18.0],
  [2.0, -1.0, -2.0, -7.0],
]);
print(matrix1 + matrix2);
// [
//  [11.0, 22.0, 33.0, 44.0],
//  [0.0, 22.0, 9.0, 26.0],
//  [11.0, -1.0, -4.0, -10.0],
// ];

Sum of a matrix and a scalar

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
print(matrix + 7);
//  [
//    [8.0, 9.0, 10.0, 11.0],
//    [12.0, 13.0, 14.0, 15.0],
//    [16.0, 7.0, 5.0, 4.0],
//  ];

Multiplication of a matrix and a vector

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
    [9.0, .0, -2.0, -3.0],
  ]);
  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0]);
  final result = matrix * vector;
  print(result); 
  // a vector-column [
  //  [40],
  //  [96],
  //  [-5],
  //]

Multiplication of a matrix and another matrix

  import 'package:ml_linalg/linalg.dart';

  final matrix1 = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
    [9.0, .0, -2.0, -3.0],
  ]);
  final matrix2 = Matrix.fromList([
    [1.0, 2.0],
    [5.0, 6.0],
    [9.0, .0],
    [-9.0, 1.0],
  ]);
  final result = matrix1 * matrix2;
  print(result);
  //[
  // [2.0, 18.0],
  // [26.0, 54.0],
  // [18.0, 15.0],
  //]

Multiplication of a matrix and a scalar

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
print(matrix * 3);
// [
//   [3.0, 6.0, 9.0, 12.0],
//   [15.0, 18.0, 21.0, 24.0],
//   [27.0, .0, -6.0, -9.0],
// ];

Hadamard product (element-wise matrices multiplication)

import 'package:ml_linalg/linalg.dart';

final matrix1 = Matrix.fromList([
  [1.0, 2.0,  3.0,  4.0],
  [5.0, 6.0,  7.0,  8.0],
  [9.0, 0.0, -2.0, -3.0],
]);
final matrix2 = Matrix.fromList([
  [7.0,   1.0,  9.0,  2.0],
  [2.0,   4.0,  3.0, -8.0],
  [0.0, -10.0, -2.0, -3.0],
]);
print(matrix1.multiply(matrix2));
// [
//   [ 7.0,  2.0, 27.0,   8.0],
//   [10.0, 24.0, 21.0, -64.0],
//   [ 0.0,  0.0,  4.0,   9.0],
// ];

Element wise matrices subtraction

import 'package:ml_linalg/linalg.dart';

final matrix1 = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
final matrix2 = Matrix.fromList([
  [10.0, 20.0, 30.0, 40.0],
  [-5.0, 16.0, 2.0, 18.0],
  [2.0, -1.0, -2.0, -7.0],
]);
print(matrix1 - matrix2);
// [
//   [-9.0, -18.0, -27.0, -36.0],
//   [10.0, -10.0, 5.0, -10.0],
//   [7.0, 1.0, .0, 4.0],
// ];

Matrix transposition

  import 'package:ml_linalg/linalg.dart';
  
  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
    [9.0, .0, -2.0, -3.0],
  ]);
  final result = matrix.transpose();
  print(result);
  //[
  // [1.0, 5.0, 9.0],
  // [2.0, 6.0, .0],
  // [3.0, 7.0, -2.0],
  // [4.0, 8.0, -3.0],
  //]

Matrix row-wise reduce

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
  ]); 
  final reduced = matrix.reduceRows((combine, row) => combine + row);
  print(reduced); // [6.0, 8.0, 10.0, 12.0]

Matrix column-wise reduce

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 17.0, 18.0],
    [21.0, 22.0, 23.0, 24.0],
  ]);
  final result = matrix.reduceColumns((combine, vector) => combine + vector);
  print(result); // [50, 66, 90]

Matrix row-wise mapping

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
  ]); 
  final modifier = Vector.filled(4, 2.0);
  final newMatrix = matrix.rowsMap((row) => row + modifier);
  print(newMatrix); 
  // [
  //  [3.0, 4.0, 5.0, 6.0],
  //  [7.0, 8.0, 9.0, 10.0],
  // ]

Matrix column-wise mapping

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
  ]); 
  final modifier = Vector.filled(2, 2.0);
  final newMatrix = matrix.columnsMap((column) => column + modifier);
  print(newMatrix); 
  // [
  //  [3.0, 4.0, 5.0, 6.0],
  //  [7.0, 8.0, 9.0, 10.0],
  // ]

Matrix element-wise mapping

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [11.0, 12.0, 13.0, 14.0],
  [15.0, 16.0, 0.0, 18.0],
  [21.0, 22.0, -23.0, 24.0],
], dtype: DType.float32);
final result = matrix.mapElements((element) => element * 2);

print(result);
// [
//  [22.0, 24.0,  26.0, 28.0],
//  [30.0, 32.0,   0.0, 36.0],
//  [42.0, 44.0, -46.0, 48.0],
// ]

Getting max value of the matrix

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 17.0, 18.0],
    [21.0, 22.0, 23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);
  final maxValue = matrix.max();
  print(maxValue);
  // 74.0

Getting min value of the matrix

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 0.0, 18.0],
    [21.0, 22.0, -23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);
  final minValue = matrix.min();
  print(minValue);
  // -23.0

Matrix element-wise power

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.pow(3.0);
  
  print(result);
  // [1 ^ 3 = 1,   2 ^ 3 = 8,   3 ^ 3 = 27 ]
  // [4 ^ 3 = 64,  5 ^ 3 = 125, 6 ^ 3 = 216]
  // [7 ^ 3 = 343, 8 ^ 3 = 512, 9 ^ 3 = 729]

Matrix element-wise exp

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.exp();
  
  print(result);
  // [e ^ 1, e ^ 2, e ^ 3]
  // [e ^ 4, e ^ 5, e ^ 6]
  // [e ^ 7, e ^ 8, e ^ 9]

Sum of all matrix elements

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.sum();
  
  print(result); // 1.0 + 2.0 + 3.0 + 4.0 + 5.0 + 6.0 + 7.0 + 8.0 + 9.0

Product of all matrix elements

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.product();
  
  print(result); // 1.0 * 2.0 * 3.0 * 4.0 * 5.0 * 6.0 * 7.0 * 8.0 * 9.0

Matrix indexing and sampling

To access a certain row vector of the matrix one may use [] operator:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 0.0, 18.0],
    [21.0, 22.0, -23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);

final row = matrix[2];

print(row); // [21.0, 22.0, -23.0, 24.0]

The library's matrix interface offers sample method that is supposed to return a new matrix, consisting of different segments of a source matrix. It's possible to build a new matrix from certain columns and vectors and they should not be necessarily subsequent.

For example, one needs to create a matrix from rows 1, 3, 5 and columns 1 and 3. To do so, it's needed to perform the following:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
//| 1 |         | 3 |                
  [4.0,   8.0,   12.0,   16.0,  34.0], // 1 Range(0, 1)
  [20.0,  24.0,  28.0,   32.0,  23.0],
  [36.0,  .0,   -8.0,   -12.0,  12.0], // 3 Range(2, 3)
  [16.0,  1.0,  -18.0,   3.0,   11.0],
  [112.0, 10.0,  34.0,   2.0,   10.0], // 5 Range(4, 5)
]);
final result = matrix.sample(
  rowIndices: [0, 2, 4],
  columnIndices: [0, 2],
);
print(result);
/*
  [4.0,   12.0],
  [36.0,  -8.0],
  [112.0, 34.0]
*/

Add new columns to a matrix

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [11.0, 12.0, 13.0, 14.0],
  [15.0, 16.0, 0.0, 18.0],
  [21.0, 22.0, -23.0, 24.0],
  [24.0, 32.0, 53.0, 74.0],
], dtype: DType.float32);

final updatedMatrix = matrix.insertColumns(0, [
  Vector.fromList([1.0, 2.0, 3.0, 4.0]),
  Vector.fromList([-1.0, -2.0, -3.0, -4.0]),
]);

print(updatedMatrix);
// [
//  [1.0, -1.0, 11.0, 12.0, 13.0, 14.0],
//  [2.0, -2.0, 15.0, 16.0, 0.0, 18.0],
//  [3.0, -3.0, 21.0, 22.0, -23.0, 24.0],
//  [4.0, -4.0, 24.0, 32.0, 53.0, 74.0],
// ]

print(updatedMatrix == matrix); // false

Matrix serialization/deserialization

To convert a matrix to a json-serializable map one may use toJson method:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 0.0, 18.0],
    [21.0, 22.0, -23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);

final serialized = matrix.toJson();

To restore a serialized matrix one may use Matrix.fromJson constructor:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromJson(serialized);

Contacts

If you have questions, feel free to write me on

• Facebook
• Linkedin