ml_linalg 13.12.6

SIMD-based linear algebra and statistics, efficient manipulation with numeric data

SIMD-based linear algebra and statistics for data science with Dart

TABLE OF CONTENTS

• What is linear algebra
• What is SIMD
• Vectors
  • A couple of words about the underlying architecture
    • Vector benchmarks
    • Vector operations
      • Vector summation
      • Vector and List summation
      • Summation of Vectors of different dtype
      • Vector subtraction
      • Vector and List subtraction
      • Subtraction of Vectors of different dtype
      • Element-wise Vector by Vector multiplication
      • Element-wise Vector and List multiplication
      • Element-wise multiplication of Vectors of different dtype
      • Element-wise Vector by Vector division
      • Element-wise Vector and List division
      • Element-wise division of Vectors of different dtype
      • Euclidean norm
      • Manhattan norm
      • Mean value
      • Median value
      • Sum of all vector elements
      • Product of all vector elements
      • Element-wise power
      • Element-wise exp
      • Dot product
      • Sum of a vector and a scalar
      • Subtraction of a scalar from a vector
      • Multiplication of a vector by a scalar
      • Division of a vector by a scalar
      • Euclidean distance between two vectors
      • Manhattan distance between two vectors
      • Cosine distance between two vectors
      • Vector normalization (using Euclidean norm)
      • Vector normalization (using Manhattan norm)
      • Vector rescaling (min-max normalization)
      • Vector serialization
      • Vector mapping
• Matrices
  • Matrix operations
    • Creation of diagonal matrix
    • Creation of scalar matrix
    • Creation of identity matrix
    • Creation of column matrix
    • Creation of row matrix
    • Sum of a matrix and another matrix
    • Sum of a matrix and a scalar
    • Multiplication of a matrix and a vector
    • Multiplication of a matrix and another matrix
    • Multiplication of a matrix and a scalar
    • Hadamard product (element-wise matrices multiplication)
    • Element-wise matrices subtraction
    • Matrix transposition
    • Matrix LU decomposition
    • Matrix Cholesky decomposition
    • Matrix LU inversion
    • Matrix Cholesky inversion
    • Lower triangular matrix inversion
    • Upper triangular matrix inversion
    • Solving a system of linear equations
    • Obtaining Matrix eigenvectors and eigenvalues, Power Iteration method
    • Matrix row-wise reduce
    • Matrix column-wise reduce
    • Matrix row-wise mapping
    • Matrix column-wise mapping
    • Matrix element-wise mapping
    • Matrix' columns filtering (by column index)
    • Matrix' columns filtering (by column)
    • Getting max value of the matrix
    • Getting min value of the matrix
    • Matrix element-wise power
    • Matrix element-wise exp
    • Sum of all matrix elements
    • Product of all matrix elements
    • Matrix indexing and sampling
    • Add new columns to a matrix
    • Matrix serialization/deserialization
• vector_math and ml_linalg differences
• Contacts

Linear algebra

In a few words, linear algebra is a branch of mathematics that works with vectors and matrices. Vectors and matrices are practical tools in real-life applications, such as machine learning algorithms. These significant mathematical entities are implemented in plenty of programming languages.

As Dart offers developers good instrumentation, e.g. highly optimized virtual machine, specific data types and rich out-of-the-box library, Dart-based implementation of vectors and matrices has to be quite performant.

Among numerous standard Dart tools, there are SIMD data types, and support of SIMD computational architecture served as inspiration for creating this library.

What is SIMD?

SIMD stands for Single instruction, multiple data - it's a computer architecture that allows to perform uniform mathematical operations in parallel on a list-like data structure. For instance, one has two arrays:

final a = [10, 20, 30, 40];
final b = [50, 60, 70, 80];

copied to clipboard

and one needs to add these arrays element-wise. Using the regular architecture this operation could be done in the following manner:

final c = List(4);

c[0] = a[0] + b[0]; // operation 1
c[1] = a[1] + b[1]; // operation 2
c[2] = a[2] + b[2]; // operation 3
c[3] = a[3] + b[3]; // operation 4

copied to clipboard

As you may have noticed, we need to do 4 operations one by one in a row using regular computational approach. But with help of SIMD architecture we may do one arithmetic operation on several operands in parallel, thus element-wise sum of two arrays can be done for just one step:

Vectors

A couple of words about the underlying architecture

The library contains two high performant vector classes based on Float32x4 and Float64x2 data types - Float32x4Vector and Float64x2Vector (the second one is generated from the source code of the first vector's implementation)

Most of element-wise operations in the first one are performed in four "threads" and in the second one - in two "threads".

Implementation of both classes is hidden from the library's users. You can create a Float32x4Vector or a Float64x2Vector instance via Vector factory (see examples below).

One can create Float32x4-based vectors the following way:

import 'package:ml_linalg/linalg.dart';

void main() {
  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0], dtype: DType.float32);
}

copied to clipboard

or simply

import 'package:ml_linalg/linalg.dart';

void main() {
  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
}

copied to clipboard

since dtype is set to DType.float32 by default.

One can create Float64x2-based vectors the following way:

import 'package:ml_linalg/linalg.dart';

void main() {
  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0], dtype: DType.float64);
}

copied to clipboard

Float32x4-based vectors are much faster than Float64x2-based ones, but Float64x2-based vectors are more precise since they use 64 bits to represent numbers in the memory versus 32 bits for Float32x4-based vectors.

Nevertheless, Float32x4 representation uses by default since usually 32 bits is enough for number precision, and along with that, this representation is more performant.

The vectors are immutable: once created, the vector cannot be changed. All the vector operations lead to creation of a new vector instance (of course, if the operation is supposed to return a Vector).

Both classes implement Iterable<double> interface, so it's possible to use them as regular iterable collections.

It's possible to use vector instances as keys for HashMap and similar data structures and to look up a value by the vector-key, since the hash code for equal vectors is the same:

import 'package:ml_linalg/vector.dart';

final map = HashMap<Vector, bool>();

map[Vector.fromList([1, 2, 3, 4, 5])] = true;

print(map[Vector.fromList([1, 2, 3, 4, 5])]); // true
print(Vector.fromList([1, 2, 3, 4, 5]).hashCode == Vector.fromList([1, 2, 3, 4, 5]).hashCode); // true

copied to clipboard

Vector benchmarks

To see the performance benefits provided by the library's vector classes, one may visit benchmark directory: one may find there a baseline benchmark - element-wise summation of two regular List instances and a benchmark of a similar operation, but performed on two Float32x4Vector instances on the same amount of elements and compare the timings:

• Baseline benchmark (executed on Macbook Air mid 2017), 2 regular lists each with 10,000,000 elements:

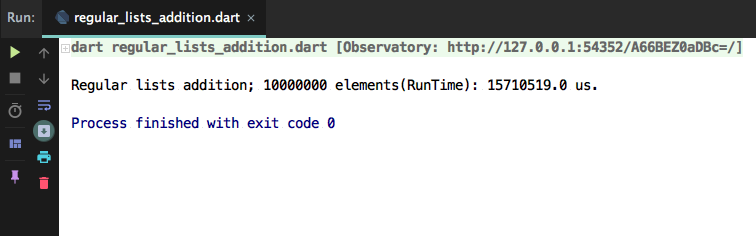
• Actual benchmark (executed on Macbook Air mid 2017), 2 vectors each with 10,000,000 elements:

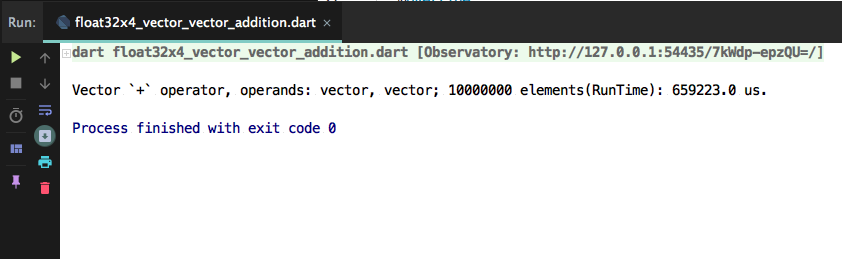
It took 15 seconds to create a new regular list by summing the elements of two lists, and 0.7 second to sum two vectors - the difference is significant.

Vector operations examples

Vector summation

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1 + vector2;

  print(result.toList()); // [3.0, 5.0, 7.0, 9.0, 11.0]

copied to clipboard

Vector and List summation

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final result = vector + [2.0, 3.0, 4.0, 5.0, 6.0];

  print(result.toList()); // [3.0, 5.0, 7.0, 9.0, 11.0]

copied to clipboard

Summation of Vectors of different dtype

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0], dtype: DType.float32);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0], dtype: DType.float64);
  final result = vector1 + vector2;

  print(result.toList()); // [3.0, 5.0, 7.0, 9.0, 11.0]

copied to clipboard

Vector subtraction

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([4.0, 5.0, 6.0, 7.0, 8.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 2.0, 3.0, 2.0]);
  final result = vector1 - vector2;

  print(result.toList()); // [2.0, 2.0, 4.0, 4.0, 6.0]

copied to clipboard

Vector and List subtraction

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([4.0, 5.0, 6.0, 7.0, 8.0]);
  final result = vector - [2.0, 3.0, 2.0, 3.0, 2.0];

  print(result.toList()); // [2.0, 2.0, 4.0, 4.0, 6.0]

copied to clipboard

Subtraction of vectors of different dtype

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([4.0, 5.0, 6.0, 7.0, 8.0], dtype: DType.float32);
  final vector2 = Vector.fromList([2.0, 3.0, 2.0, 3.0, 2.0], dtype: DType.float64);
  final result = vector1 - vector2;

  print(result.toList()); // [2.0, 2.0, 4.0, 4.0, 6.0]

copied to clipboard

Element wise Vector by Vector multiplication

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1 * vector2;

  print(result.toList()); // [2.0, 6.0, 12.0, 20.0, 30.0]

copied to clipboard

Element wise Vector and List multiplication

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final result = vector * [2.0, 3.0, 4.0, 5.0, 6.0];

  print(result.toList()); // [2.0, 6.0, 12.0, 20.0, 30.0]

copied to clipboard

Element wise multiplication of Vectors of different dtype

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0], dtype: DType.float32);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0], dtype: DType.float64);
  final result = vector1 * vector2;

  print(result.toList()); // [2.0, 6.0, 12.0, 20.0, 30.0]

copied to clipboard

Element wise Vector by Vector division

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([6.0, 12.0, 24.0, 48.0, 96.0]);
  final vector2 = Vector.fromList([3.0, 4.0, 6.0, 8.0, 12.0]);
  final result = vector1 / vector2;

  print(result.toList()); // [2.0, 3.0, 4.0, 6.0, 8.0]

copied to clipboard

Element-wise Vector and List division

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([6.0, 12.0, 24.0, 48.0, 96.0]);
  final result = vector / [3.0, 4.0, 6.0, 8.0, 12.0];

  print(result.toList()); // [2.0, 3.0, 4.0, 6.0, 8.0]

copied to clipboard

Element wise division of vectors of different dtype

This operation doesn't benefit from SIMD

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([6.0, 12.0, 24.0, 48.0, 96.0], dtype: DType.float32);
  final vector2 = Vector.fromList([3.0, 4.0, 6.0, 8.0, 12.0], dtype: DType.float64);
  final result = vector1 / vector2;

  print(result.toList()); // [2.0, 3.0, 4.0, 6.0, 8.0]

copied to clipboard

Euclidean norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.norm();

  print(result); // sqrt(2^2 + 3^2 + 4^2 + 5^2 + 6^2) = sqrt(90) ~~ 9.48

copied to clipboard

Manhattan norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.norm(Norm.manhattan);

  print(result); // 2 + 3 + 4 + 5 + 6 = 20.0

copied to clipboard

Mean value

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.mean();

  print(result); // (2 + 3 + 4 + 5 + 6) / 5 = 4.0

copied to clipboard

Median value

Even length

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([10, 12, 4, 7, 9, 12]);
  final result = vector.median();

  print(result); // 9.5

copied to clipboard

Odd length

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([10, 12, 4, 7, 9, 12, 34]);
  final result = vector.median();

  print(result); // 10

copied to clipboard

Sum of all vector elements

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.sum();

  print(result); // 2 + 3 + 4 + 5 + 6 = 20.0

copied to clipboard

Product of all vector elements

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.prod();

  print(result); // 2 * 3 * 4 * 5 * 6 = 720

copied to clipboard

Element-wise power

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.pow(3);
  
  print(result); // [2 ^ 3 = 8.0, 3 ^ 3 = 27.0, 4 ^ 3 = 64.0, 5 ^3 = 125.0, 6 ^ 3 = 216.0]

copied to clipboard

Element-wise exp

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector.exp();
  
  print(result); // [e ^ 2, e ^ 3, e ^ 4, e ^ 5, e ^ 6]

copied to clipboard

Dot product of two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.dot(vector2);

  print(result); // 1.0 * 2.0 + 2.0 * 3.0 + 3.0 * 4.0 + 4.0 * 5.0 + 5.0 * 6.0 = 70.0

copied to clipboard

Sum of a vector and a scalar

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final scalar = 5.0;
  final result = vector + scalar;

  print(result.toList()); // [6.0, 7.0, 8.0, 9.0, 10.0]

copied to clipboard

Subtraction of a scalar from a vector

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final scalar = 5.0;
  final result = vector - scalar;

  print(result.toList()); // [-4.0, -3.0, -2.0, -1.0, 0.0]

copied to clipboard

Multiplication of a vector by a scalar

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final scalar = 5.0;
  final result = vector * scalar;

  print(result.toList()); // [5.0, 10.0, 15.0, 20.0, 25.0]

copied to clipboard

Division of a vector by a scalar

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([25.0, 50.0, 75.0, 100.0, 125.0]);
  final scalar = 5.0;
  final result = vector.scalarDiv(scalar);

  print(result.toList()); // [5.0, 10.0, 15.0, 20.0, 25.0]

copied to clipboard

Euclidean distance between two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.distanceTo(vector2, distance: Distance.euclidean);

  print(result); // ~~2.23

copied to clipboard

Manhattan distance between two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.distanceTo(vector2, distance: Distance.manhattan);

  print(result); // 5.0

copied to clipboard

Cosine distance between two vectors

  import 'package:ml_linalg/linalg.dart';

  final vector1 = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final vector2 = Vector.fromList([2.0, 3.0, 4.0, 5.0, 6.0]);
  final result = vector1.distanceTo(vector2, distance: Distance.cosine);

  print(result); // 0.00506

copied to clipboard

Vector normalization using Euclidean norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, 2.0, 3.0, 4.0, 5.0]);
  final result = vector.normalize(Norm.euclidean);

  print(result); // [0.134, 0.269, 0.404, 0.539, 0.674]

copied to clipboard

Vector normalization using Manhattan norm

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0]);
  final result = vector.normalize(Norm.manhattan);

  print(result); // [0.066, -0.133, 0.200, -0.266, 0.333]

copied to clipboard

Vector rescaling (min-max normalization)

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0, 0.0]);
  final result = vector.rescale();

  print(result); // [0.555, 0.222, 0.777, 0.0, 1.0, 0.444]

copied to clipboard

Vector serialization

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0, 0.0]);
  final serialized = vector.toJson();
  print(serialized); // it yields a serializable representation of the vector

  final restoredVector = Vector.fromJson(serialized);
  print(restoredVector); // [1.0, -2.0, 3.0, -4.0, 5.0, 0.0]

copied to clipboard

Vector mapping

  import 'package:ml_linalg/linalg.dart';

  final vector = Vector.fromList([1.0, -2.0, 3.0, -4.0, 5.0, 0.0]);
  final mapped = vector.mapToVector((el) => el * 2);
  
  print(mapped); // [2.0, -4.0, 6.0, -8.0, 10.0, 0.0]
  print(mapped is Vector); // true
  print(identical(vector, mapped)); // false

copied to clipboard

Matrices

Along with SIMD vectors, the library contains SIMD-based Matrices. One can use the matrices via Matrix factory. The matrices are immutable as well as vectors and also they implement Iterable interface (to be more precise, Iterable<Iterable<double>>), thus it's possible to use them as a regular iterable collection.

Matrices are serializable, and that means that one can easily convert a Matrix instance to a json-serializable map via toJson method, see the examples below.

Matrix operations examples

Creation of diagonal matrix

import 'package:ml_linalg/matrix.dart';

final matrix = Matrix.diagonal([1, 2, 3, 4, 5]);

print(matrix);

copied to clipboard

The output:

Matrix 5 x 5:
(1.0, 0.0, 0.0, 0.0, 0.0)
(0.0, 2.0, 0.0, 0.0, 0.0)
(0.0, 0.0, 3.0, 0.0, 0.0)
(0.0, 0.0, 0.0, 4.0, 0.0)
(0.0, 0.0, 0.0, 0.0, 5.0)

copied to clipboard

Creation of scalar matrix

import 'package:ml_linalg/matrix.dart';

final matrix = Matrix.scalar(3, 5);

print(matrix);

copied to clipboard

The output:

Matrix 5 x 5:
(3.0, 0.0, 0.0, 0.0, 0.0)
(0.0, 3.0, 0.0, 0.0, 0.0)
(0.0, 0.0, 3.0, 0.0, 0.0)
(0.0, 0.0, 0.0, 3.0, 0.0)
(0.0, 0.0, 0.0, 0.0, 3.0)

copied to clipboard

Creation of identity matrix

import 'package:ml_linalg/matrix.dart';

final matrix = Matrix.identity(5);

print(matrix);

copied to clipboard

The output:

Matrix 5 x 5:
(1.0, 0.0, 0.0, 0.0, 0.0)
(0.0, 1.0, 0.0, 0.0, 0.0)
(0.0, 0.0, 1.0, 0.0, 0.0)
(0.0, 0.0, 0.0, 1.0, 0.0)
(0.0, 0.0, 0.0, 0.0, 1.0)

copied to clipboard

Creation of column matrix

final matrix = Matrix.column([1, 2, 3, 4, 5]);

print(matrix);

copied to clipboard

The output:

Matrix 5 x 1:
(1.0)
(2.0)
(3.0)
(4.0)
(5.0)

copied to clipboard

Creation of row matrix

final matrix = Matrix.row([1, 2, 3, 4, 5]);

print(matrix);

copied to clipboard

The output:

Matrix 1 x 5:
(1.0, 2.0, 3.0, 4.0, 5.0)

copied to clipboard

Sum of a matrix and another matrix

import 'package:ml_linalg/linalg.dart';

final matrix1 = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
final matrix2 = Matrix.fromList([
  [10.0, 20.0, 30.0, 40.0],
  [-5.0, 16.0, 2.0, 18.0],
  [2.0, -1.0, -2.0, -7.0],
]);
print(matrix1 + matrix2);
// [
//  [11.0, 22.0, 33.0, 44.0],
//  [0.0, 22.0, 9.0, 26.0],
//  [11.0, -1.0, -4.0, -10.0],
// ];

copied to clipboard

Sum of a matrix and a scalar

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
print(matrix + 7);
//  [
//    [8.0, 9.0, 10.0, 11.0],
//    [12.0, 13.0, 14.0, 15.0],
//    [16.0, 7.0, 5.0, 4.0],
//  ];

copied to clipboard

Multiplication of a matrix and a vector

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
    [9.0, .0, -2.0, -3.0],
  ]);
  final vector = Vector.fromList([2.0, 3.0, 4.0, 5.0]);
  final result = matrix * vector;
  print(result); 
  // a vector-column [
  //  [40],
  //  [96],
  //  [-5],
  //]

copied to clipboard

Multiplication of a matrix and another matrix

  import 'package:ml_linalg/linalg.dart';

  final matrix1 = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
    [9.0, .0, -2.0, -3.0],
  ]);
  final matrix2 = Matrix.fromList([
    [1.0, 2.0],
    [5.0, 6.0],
    [9.0, .0],
    [-9.0, 1.0],
  ]);
  final result = matrix1 * matrix2;
  print(result);
  //[
  // [2.0, 18.0],
  // [26.0, 54.0],
  // [18.0, 15.0],
  //]

copied to clipboard

Multiplication of a matrix and a scalar

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
print(matrix * 3);
// [
//   [3.0, 6.0, 9.0, 12.0],
//   [15.0, 18.0, 21.0, 24.0],
//   [27.0, .0, -6.0, -9.0],
// ];

copied to clipboard

Hadamard product (element-wise matrices multiplication)

import 'package:ml_linalg/linalg.dart';

final matrix1 = Matrix.fromList([
  [1.0, 2.0,  3.0,  4.0],
  [5.0, 6.0,  7.0,  8.0],
  [9.0, 0.0, -2.0, -3.0],
]);
final matrix2 = Matrix.fromList([
  [7.0,   1.0,  9.0,  2.0],
  [2.0,   4.0,  3.0, -8.0],
  [0.0, -10.0, -2.0, -3.0],
]);
print(matrix1.multiply(matrix2));
// [
//   [ 7.0,  2.0, 27.0,   8.0],
//   [10.0, 24.0, 21.0, -64.0],
//   [ 0.0,  0.0,  4.0,   9.0],
// ];

copied to clipboard

Element wise matrices subtraction

import 'package:ml_linalg/linalg.dart';

final matrix1 = Matrix.fromList([
  [1.0, 2.0, 3.0, 4.0],
  [5.0, 6.0, 7.0, 8.0],
  [9.0, .0, -2.0, -3.0],
]);
final matrix2 = Matrix.fromList([
  [10.0, 20.0, 30.0, 40.0],
  [-5.0, 16.0, 2.0, 18.0],
  [2.0, -1.0, -2.0, -7.0],
]);
print(matrix1 - matrix2);
// [
//   [-9.0, -18.0, -27.0, -36.0],
//   [10.0, -10.0, 5.0, -10.0],
//   [7.0, 1.0, .0, 4.0],
// ];

copied to clipboard

Matrix transposition

  import 'package:ml_linalg/linalg.dart';
  
  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
    [9.0, .0, -2.0, -3.0],
  ]);
  final result = matrix.transpose();
  print(result);
  //[
  // [1.0, 5.0, 9.0],
  // [2.0, 6.0, .0],
  // [3.0, 7.0, -2.0],
  // [4.0, 8.0, -3.0],
  //]

copied to clipboard

Matrix LU decomposition

  final matrix = Matrix.fromList([
    [4, 12, -16],
    [12, 37, -43],
    [-16, -43, 98],
  ], dtype: dtype);
  final decomposed = matrix.decompose(Decomposition.LU);
  
  // yields approximately the same matrix as the original one:
  print(decomposed.first * decomposed.last);

copied to clipboard

Matrix Cholesky decomposition

  final matrix = Matrix.fromList([
    [4, 12, -16],
    [12, 37, -43],
    [-16, -43, 98],
  ], dtype: dtype);
  final decomposed = matrix.decompose(Decomposition.cholesky);
  
  // yields approximately the same matrix as the original one:
  print(decomposed.first * decomposed.last);

copied to clipboard

Keep in mind that Cholesky decomposition is applicable only for positive definite and symmetric matrices

Matrix LU inversion

  final matrix = Matrix.fromList([
    [-16, -43, 98],
    [33, 12.4, 37],
    [12, -88.3, 4],
  ], dtype: dtype);
  final inverted = matrix.inverse(Inverse.LU);

  print(inverted * matrix);
  // The output (there can be some round-off errors):
  // [1, 0, 0],
  // [0, 1, 0],
  // [0, 0, 1],

copied to clipboard

Matrix Cholesky inversion

  final matrix = Matrix.fromList([
    [4, 12, -16],
    [12, 37, -43],
    [-16, -43, 98],
  ], dtype: dtype);
  final inverted = matrix.inverse(Inverse.cholesky);

  print(inverted * matrix);
  // The output (there can be some round-off errors):
  // [1, 0, 0],
  // [0, 1, 0],
  // [0, 0, 1],

copied to clipboard

Keep in mind that since this kind of inversion is based on Cholesky decomposition, the inversion is applicable only for positive definite and symmetric matrices

Lower triangular matrix inversion

  final matrix = Matrix.fromList([
    [  4,   0,  0],
    [ 12,  37,  0],
    [-16, -43, 98],
  ], dtype: dtype);
  final inverted = matrix.inverse(Inverse.forwardSubstitution);

  print(inverted * matrix);
  // The output (there can be some round-off errors):
  // [1, 0, 0],
  // [0, 1, 0],
  // [0, 0, 1],

copied to clipboard

Upper triangular matrix inversion

  final matrix = Matrix.fromList([
    [4, 12, -16],
    [0, 37, -43],
    [0,  0, -98],
  ], dtype: dtype);
  final inverted = matrix.inverse(Inverse.backwardSubstitution);

  print(inverted * matrix);
  // The output (there can be some round-off errors):
  // [1, 0, 0],
  // [0, 1, 0],
  // [0, 0, 1],

copied to clipboard

Solving a system of linear equations

A matrix notation for a system of linear equations:

AX=B

copied to clipboard

To solve the system and find X, one may use the solve method:

import 'package:ml_linalg/linalg.dart';

void main() {
  final A = Matrix.fromList([
    [1, 1, 1],
    [0, 2, 5],
    [2, 5, -1],
  ], dtype: dtype);
  final B = Matrix.fromList([
    [6],
    [-4],
    [27],
  ], dtype: dtype);
  final result = A.solve(B);
  
  print(result); // the output is close to [[5], [3], [-2]]
}

copied to clipboard

Obtaining Matrix eigenvectors and eigenvalues, Power Iteration method

The method returns a collection of pairs of an eigenvector and its corresponding eigenvalue. By default Power iteration method is used.

  final matrix = Matrix.fromList([
    [1, 0],
    [0, 2],
  ]);
  final eigen = matrix.eigen();
  
  print(eigen); // It prints the following: [Value: 1.999, Vector: (0.001, 0.999);]

copied to clipboard

Matrix row-wise reduce

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
  ]); 
  final reduced = matrix.reduceRows((combine, row) => combine + row);
  print(reduced); // [6.0, 8.0, 10.0, 12.0]

copied to clipboard

Matrix column-wise reduce

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 17.0, 18.0],
    [21.0, 22.0, 23.0, 24.0],
  ]);
  final result = matrix.reduceColumns((combine, vector) => combine + vector);
  print(result); // [50, 66, 90]

copied to clipboard

Matrix row-wise mapping

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
  ]); 
  final modifier = Vector.filled(4, 2.0);
  final newMatrix = matrix.rowsMap((row) => row + modifier);
  print(newMatrix); 
  // [
  //  [3.0, 4.0, 5.0, 6.0],
  //  [7.0, 8.0, 9.0, 10.0],
  // ]

copied to clipboard

Matrix column-wise mapping

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0, 4.0],
    [5.0, 6.0, 7.0, 8.0],
  ]); 
  final modifier = Vector.filled(2, 2.0);
  final newMatrix = matrix.columnsMap((column) => column + modifier);
  print(newMatrix); 
  // [
  //  [3.0, 4.0, 5.0, 6.0],
  //  [7.0, 8.0, 9.0, 10.0],
  // ]

copied to clipboard

Matrix element-wise mapping

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [11.0, 12.0, 13.0, 14.0],
  [15.0, 16.0, 0.0, 18.0],
  [21.0, 22.0, -23.0, 24.0],
], dtype: DType.float32);
final result = matrix.mapElements((element) => element * 2);

print(result);
// [
//  [22.0, 24.0,  26.0, 28.0],
//  [30.0, 32.0,   0.0, 36.0],
//  [42.0, 44.0, -46.0, 48.0],
// ]

copied to clipboard

Matrix' columns filtering (by column index)

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [11.0, 12.0, 13.0, 14.0],
  [15.0, 16.0, 17.0, 18.0],
  [21.0, 22.0, 23.0, 24.0],
], dtype: dtype);

final indicesToExclude = [0, 3];
final result = matrix.filterColumns((column, idx) => !indicesToExclude.contains(idx));

print(result);
// [
//   [12.0, 13.0],
//   [16.0, 17.0],
//   [22.0, 23.0],
// ]

copied to clipboard

Matrix' columns filtering (by column)

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [11.0, 33.0, 13.0, 14.0],
  [15.0, 92.0, 17.0, 18.0],
  [21.0, 22.0, 23.0, 24.0],
], dtype: dtype);

final result = matrix.filterColumns((column, _) => column.sum() > 100);

print(result);
// [
//   [33.0],
//   [92.0],
//   [22.0],
// ];

copied to clipboard

Getting max value of the matrix

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 17.0, 18.0],
    [21.0, 22.0, 23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);
  final maxValue = matrix.max();
  print(maxValue);
  // 74.0

copied to clipboard

Getting min value of the matrix

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 0.0, 18.0],
    [21.0, 22.0, -23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);
  final minValue = matrix.min();
  print(minValue);
  // -23.0

copied to clipboard

Matrix element-wise power

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.pow(3.0);
  
  print(result);
  // [1 ^ 3 = 1,   2 ^ 3 = 8,   3 ^ 3 = 27 ]
  // [4 ^ 3 = 64,  5 ^ 3 = 125, 6 ^ 3 = 216]
  // [7 ^ 3 = 343, 8 ^ 3 = 512, 9 ^ 3 = 729]

copied to clipboard

Matrix element-wise exp

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.exp();
  
  print(result);
  // [e ^ 1, e ^ 2, e ^ 3]
  // [e ^ 4, e ^ 5, e ^ 6]
  // [e ^ 7, e ^ 8, e ^ 9]

copied to clipboard

Sum of all matrix elements

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.sum();
  
  print(result); // 1.0 + 2.0 + 3.0 + 4.0 + 5.0 + 6.0 + 7.0 + 8.0 + 9.0

copied to clipboard

Product of all matrix elements

  import 'package:ml_linalg/linalg.dart';

  final matrix = Matrix.fromList([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0],
    [7.0, 8.0, 9.0],
  ]);
  final result = matrix.product();
  
  print(result); // 1.0 * 2.0 * 3.0 * 4.0 * 5.0 * 6.0 * 7.0 * 8.0 * 9.0

copied to clipboard

Matrix indexing and sampling

To access a certain row vector of the matrix one may use [] operator:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 0.0, 18.0],
    [21.0, 22.0, -23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);

final row = matrix[2];

print(row); // [21.0, 22.0, -23.0, 24.0]

copied to clipboard

The library's matrix interface offers sample method that is supposed to return a new matrix, consisting of different segments of a source matrix. It's possible to build a new matrix from certain columns and vectors and they should not be necessarily subsequent.

For example, one needs to create a matrix from rows 1, 3, 5 and columns 1 and 3. To do so, it's needed to perform the following:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
//| 1 |         | 3 |                
  [4.0,   8.0,   12.0,   16.0,  34.0], // 1 Range(0, 1)
  [20.0,  24.0,  28.0,   32.0,  23.0],
  [36.0,  .0,   -8.0,   -12.0,  12.0], // 3 Range(2, 3)
  [16.0,  1.0,  -18.0,   3.0,   11.0],
  [112.0, 10.0,  34.0,   2.0,   10.0], // 5 Range(4, 5)
]);
final result = matrix.sample(
  rowIndices: [0, 2, 4],
  columnIndices: [0, 2],
);
print(result);
/*
  [4.0,   12.0],
  [36.0,  -8.0],
  [112.0, 34.0]
*/

copied to clipboard

Add new columns to a matrix

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
  [11.0, 12.0, 13.0, 14.0],
  [15.0, 16.0, 0.0, 18.0],
  [21.0, 22.0, -23.0, 24.0],
  [24.0, 32.0, 53.0, 74.0],
], dtype: DType.float32);

final updatedMatrix = matrix.insertColumns(0, [
  Vector.fromList([1.0, 2.0, 3.0, 4.0]),
  Vector.fromList([-1.0, -2.0, -3.0, -4.0]),
]);

print(updatedMatrix);
// [
//  [1.0, -1.0, 11.0, 12.0, 13.0, 14.0],
//  [2.0, -2.0, 15.0, 16.0, 0.0, 18.0],
//  [3.0, -3.0, 21.0, 22.0, -23.0, 24.0],
//  [4.0, -4.0, 24.0, 32.0, 53.0, 74.0],
// ]

print(updatedMatrix == matrix); // false

copied to clipboard

Matrix serialization/deserialization

To convert a matrix to a json-serializable map one may use toJson method:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromList([
    [11.0, 12.0, 13.0, 14.0],
    [15.0, 16.0, 0.0, 18.0],
    [21.0, 22.0, -23.0, 24.0],
    [24.0, 32.0, 53.0, 74.0],
  ]);

final serialized = matrix.toJson();

copied to clipboard

To restore a serialized matrix one may use Matrix.fromJson constructor:

import 'package:ml_linalg/linalg.dart';

final matrix = Matrix.fromJson(serialized);

copied to clipboard

Differences between vector math and ml linalg

There are similar solutions on the internet, the most famous of which is vector_math by the Google team. At first glance, vector_math and ml_linalg look similar - both of them are based on SIMD, but in fact, these are two completely different libraries:

vector_math supports only four dimensions for vectors and matrices at max; ml_linalg can handle vectors and matrices of potentially infinite length, keeping SIMD nature.

Contacts

If you have questions, feel free to write me on

• Twitter
• Facebook
• Linkedin