Sample Statistics

Dart

Introduction

The package sample_statistics provides helpers for calculating statistics of numerical samples and generating/exporting histograms. It includes common probability distribution functions, an approximation of the error function, and random sample generators.

Throughout the library the acronym Pdf stands for Probability Distribution Function, while Cdf stands for Cummulative Distribution Function.

Usage

To use this package include sample_statistics as a dependency in your pubspec.yaml file.

1. Sample Statistics

To access sample statistics use the class Stats. It calculates sample statistics in a lazy fashion and caches results to avoid expensive calculations if the same quantity is accessed repeatedly. If the random sample changes use the method updateCache() to recalculate the sample statistics.

 import 'package:sample_statistics/sample_statistics.dart'

 void main() {

   final sample = <num>[-10, 0, 1, 2, 3, 4, 5, 6, 20]
   final stats = Stats(sample)

   print('\nRunning statistic_example.dart ...')
   print('Sample: $sample')
   print('min: ${stats.min}')
   print('max:  ${stats.max}')
   print('mean: ${stats.mean}')
   print('median: ${stats.median}')
   print('first quartile:  ${stats.quartile1}')
   print('third quartile:  ${stats.quartile3}')
   print('standard deviation:  ${stats.stdDev}')

   final outliers = sample.removeOutliers();
   print('outliers: $outliers')
   print('sample with outliers removed:  $sample');

   // Update statistics after sample has changed:
   stats.updateCache();
 }
Click to show console output. 
 $ dart  sample_statistics_example.dart

 Running sample_statistic_example.dart ...
 Sample: [-10, 0, 1, 2, 3, 4, 5, 6, 20]
 min: -10
 max: 20
 mean: 3.4444444444444446
 median: 3
 first quartile: 1
 third quartile: 5
 standard deviation: 7.779960011322538
 outliers:[-10, 20]
 sample with outliers removed: [0, 1, 2, 3, 4, 5, 6]

2. Random Sample Generators

The library sample_generators includes functions for generating random samples that follow the probability distribution functions listed below:

  • normal distribution,
  • truncated normal distribution,
  • exponential distribution,
  • uniform distribution,
  • triangular distribution.

Additionally, the library includes the function randomSample which is based on the rejection sampling method. It expects a callback of type ProbabilityDensity and can be used to generate random samples that follow an arbitrary probability distribution function.

The program listed below demonstrates how to generated a random sample and write a histogram to a file.

import 'dart:io';

 import 'package:sample_statistics/sample_statistics.dart';

 void main(List<String> args) async{
   final xMmin = 1.0;
   final xMmax = 9.0;
   final meanOfParent = 5.0;
   final stdDevOfParent = 2.0;
   final sampleSize = 1000;

   // Generating the random sample with 1000 entries.
   final sample = truncatedNormalSample(
     sampleSize,
     xMmin,
     xMmax,
     meanOfParent,
     stdDevOfParent,
   );

   final stats = Stats(sample);
   print(stats.mean);
   print(stats.stdDev);
   print(stats.min);

   // Exporting a histogram.
   // Export histogram
   await File('example/data/truncated_normal$sampleSize.hist').writeAsString(
     sample.exportHistogram(
       pdf: (x) =>
           truncatedNormalPdf(x, xMin, xMax, meanOfParent, stdDevOfParent),
     ),
   );

 }

3. Generating Histograms

To generate a histogram, the first step consists in dividing the random sample range into a suitable number of intervals. The second step consists in counting how many sample entries fall into each interval.

The figures below show the histograms obtained from two random samples that follow a truncated normal distribution with xMin = 2.0, xMax = 6.0 and normal parent distribution with meanOfParent = 3.0, and stdDevOfParent = 1.0. The random samples were generated using the function truncatedNormalSample. The histograms were generated using the extension method exportHistogram, see source code above.

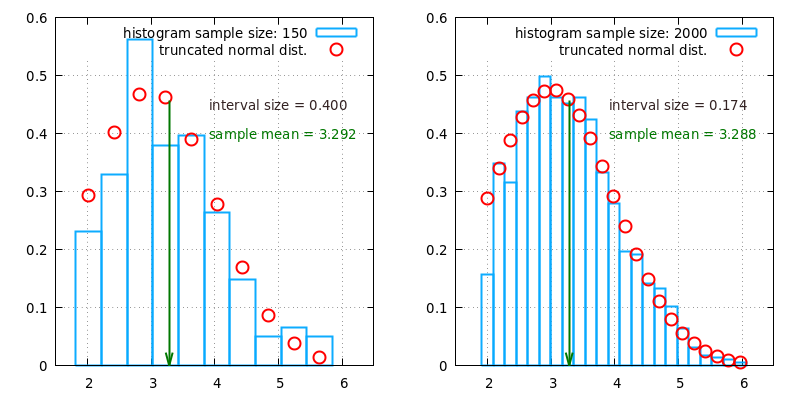
Histogram

The figure on the left shows the histogram of a sample with size 150. The figure on the right shows the histogram of a sample with size 600. Increasing the random sample size leads to an increasingly closer match between the shape of the histogram and the underlying probability distribution.

Using the distribution parameters mentioned above with the function meanTruncatedNormal, one can determine a theoretical mean of 3.2828. It can be seen that in the limit of a large sample size the sample mean approaches the mean of the underlying probability distribution.

Examples

For further examples on how to generate random samples, export histograms, and access sample statistics see folder example.

Features and bugs

Please file feature requests and bugs at the issue tracker.

Libraries

sample_statistics